빅오(Big - O)표기법

 

 

youtu.be/6Iq5iMCVsXA

---

빅오 : 알고리즘의 성능을 수학적으로 표기한것(시간 / 공간복잡도)

 

실제 러닝타임이 아니라 알고리즘의 성능을 예측하는것이 목표이다.

상수와 같은 숫자들은 1이 된다.

 

1. O(1)

F(int[] n){
  return (n[0] == 0)? true : false;
}

(저 인자로 받는 값의 크기가 얼마이냐에 상관없이 배열의 첫번째 값이 0인지를 확인하는건데, 언제나 일정한 속도로 결과를 반환한다.)

 

입력데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘을 말한다.

데이터가 증가함에 따라 성능에 변함이 없다.

 

2. O(n) 데이터와 시간이 같은 비율로 증가

 

F(int[] n) {
	for i = 0 to n.length
    	print i
}

(n개의 데이터를 받으면 n번 루프를 도니까 n이 하나 늘어날때마다 처리가 한번씩 늘어나서 n의 크기만큼 처리시간이 걸린다.)

입력 데이터의 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현할때 사용한다.

데이터가 증가함에 따라 처리 시간도 비례해서 증가한다.

 

3. O(n2)

F(int[] n){
	for i = 0 to n.length
    	for j = 0 to n.length
        	print i + j;
}

n을 돌리면서 n으로 루프를 또 돌릴때 n square가 된다.

n이 가로세로 면적만큼의 길이로 는다.

n이 하나 늘어날때마다 아래한줄 오른쪽에 한줄 n만큼씩 주르륵 붙는다.

데이터가 커질수록 데이터 처리시간의 부담도 커진다.

 

처음에는 조금씩 상승하다가 나중에는 그래프가 수직상승이 된다.

 

4. O(nm)

F(int[] n , int[] m){
	for i = to  n.length
    	for j = 0 to m.length
        	print i + j;
}

 

코드가 0(n2)와 비슷하지만 n을 두번 돌리는게 아니라 m을 n만큼 두 번 돌리는것을 의미한다.

(루프모양보고 0(n2)와 착각해서는 안된다!)

 

n은 엄청크고 m을 아주 작을수도 있기 때문에 변수가 다르다면 빅오 표기법에도 반드시 다르게 표기를 해줘야 한다.

데이터가 증가할수록 그래프가 점점 수직에 가까운 모양이 된다.

 

 

5. O(n3)

F(int[] n){
	for i = 0 to n.length
    	for j = 0 to n.length
        	for k = 0 to n.length
            	print i + j + k;
}

n의 제곱에 n을 한번 더 돌린것이다.

루프를 n을 가지고 삼중으로 돌리면 n의 세제곱이 된다.

 

On일때는 아래와 같이 직선이였고,

 

n의 제곱일때는 면적이였다.

 

n의 세제곱은 n의 제곱을 n만큼 더 돌리니까 큐빅이 된다.

n제곱과 비슷한 양상을 보이지만 데이터가 늘어날때마다 가로세로의 높이까지 더해지니까 아무래도 데이터가 증가함에 따라 급격하게 처리 시간이 늘어나는것을 볼 수 있다.

6. O(2n)

 

n의 2승과 2의 n승은 햇갈리게 생겼는데 둘은 너무나 다른 알고리즘이다.

피보나치 수열을 생각해본다.

1부터 시작해서 한면을 기준으로 정사각형을 만든다.

F(n, r) {
	if (n <= 0) return 0;
    else if (n == 1) return r[n] = 1;
    return r[n] = F(n - 1, r) + F(n - 2, r);
}

(피보나치 수열을 재귀함수를 이용해서 구현한 모습)

 

함수를 호출할때 마다 바로 전의 숫자랑 전전 숫자를 알아야 더할수가 있으므로 해당 숫자를 알아내기 위해서

하나뺀 숫자를 가지고 재귀호출을 하고 두개뺀 숫자를 가지고 한번 더 호출을 한다.

그걸 트리의 높이만큼 반복한다.

 

 

데이터의 증가에 따라 처리시간이 현저하게 증가하는것을 볼 수 있다.

 

 

7.  O(mn)  : m개씩 n번 늘어나는 알고리즘(2대신에 m을 써서 표현하면 된다.)

 

8. O(log n)

 

대표적인 이진검색

 

정렬이 된 array에서 6을 찾아보자.

우선 가운데 값을 찾아서 key인 6 하고 비교를 한다.

그 다음에 뒤쪽에 있는 값의 중간값과 키 값을 비교한다.

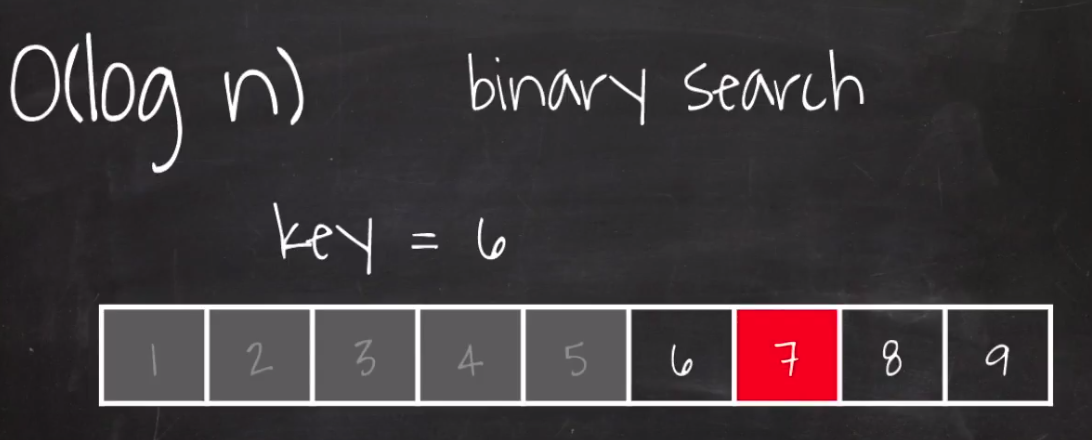
이렇게 한번 처리가 진행될때마다 검색해야될 데이터 양이 절반씩 뚝뚝 떨어진다.

F(k, arr, s, e) {
	if(s > e) return -1 ;
    m = (s + e) / 2;
    if(arr[m] == k) return m;
    else if (arr[m] > k) return F(k, arr, s, m-1);
    else return F(k, arr, m+1, e);
}

처음 호출될때 시작시작부분인 s는 0, 끝지점인 m은 배열의 맨 마지막

주어진 array의 중간값을 찾는다.

찾는값이 중간값보다 작으면 중간지점 바로 전까지 array를 조정해서 다시 호출한다.

키 값이 중간값보다 크면 중간지점 다음방부터 맨 끝인 e까지 호출한다.

이렇게 함수를 호출할때마다 절반은 검색영역에서 제외시키므로 속도가 빠르다.

 

O(n)보다 적게 드는것을 볼 수 있는데 ,데이터가 증가해도 성능에 크게 차이가 없다.

 

9. O(sqrt(n))

 

제곱근이란?

 

100의 제곱근은 10이다. 10을 두번 곱한것이므로

저 n을 정사각형에 채워서 저 위에 한줄이 제곱근이다.

n으로 9를 받으면?

맨 위의 한줄이 제곱근이 된다.

 

이번에는 n이 16이라면?

 

이번에도 맨 위의 한줄이 제곱근이 되는걸 볼 수 있다.

---

마지막으로 빅오에서 중요한것을 말하자면

빅오에서는 상수는 과감하게 버린다. 

 

아래 코드의 시간 복잡도는? O(?)

F(int[] n) {
	for i = 0 to n.length
    	print i
    for i = 0 to n.length
    	print i
}

2n이라고 생각할 수 있는 빅오 표기법에서 2n은 n으로 표시한다.

O(2n) => O(n)

왜냐하면 빅오 표기법은 실제 알고리즘의 러닝타임을 재기위해 만든것이 아니라 단기적으로 데이터가 증가함에 따라 처리율의 예측을 위해서 만들어진 표기법이라 그렇다.

상수는 고정된 숫자니까 증가율에 영향을 미칠때 언제나 고정된 상수만큼씩만 영향을 미치기 때문에

여기서 증가하지 않는 숫자는 신경쓰지 않겠다는것이다.

 

F(int[] n) {
	for i = 0 to n.length
    	for j = 0 to n.length
        	print i + j;
    for i = 0 to n.length
    	for j = 0 to n.length
        	print i + j;
}

 n의 제곱도 앞의 붙는 상수는 무시하고 2n의 제곱도 n의 제곱으로 써주면 된다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

※ 본 포스팅은 개인 공부 기록을 목적으로 남긴 글이며 본 사실과 다른 부분이 있다면 과감하게 지적 부탁드립니다.